How To Calculate Horizontal Tangent Line

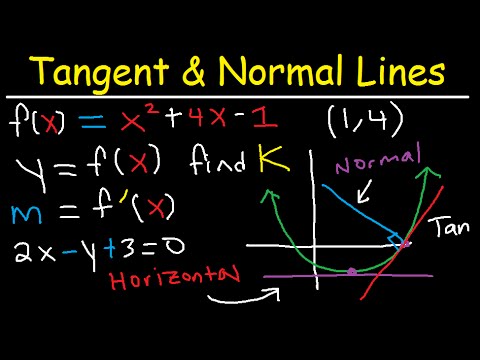
A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. This is because, by definition, the derivative gives the slope of the tangent line. Therefore, when the derivative is zero, the tangent line is horizontal.

To find horizontal tangent lines, use the derivative of the function to locate the zeros and plug them back into the original equation. Horizontal tangent lines are important in calculus because they indicate local maximum or minimum points in the original function. A horizontal tangent is parallel to x-axis and hence its slope is zero. We know that the slope is nothing but the derivative of the function.

So to find the points where there are horizontal tangents just set the derivative of the function to zero and solve. After getting the points, we can find the equation of the horizontal tangent line using the point-slope form. The tangent line of a curve at a given point is a line that just touches the curve at that point.

The tangent line in calculus may touch the curve at any other point and it also may cross the graph at some other point as well. Here, we can see some examples of tangent lines and secant lines. A horizontal tangent line is parallel to the x-axis and shows where a function has a slope of zero. You can find these lines either by looking at a graph or by setting an equation to zero to find maximums and minimums.

A vertical tangent is parallel to y-axis and hence its slope is undefined. After getting the points, we can find the equation of the vertical tangent line using the point-slope form. The "tangent line" is one of the most important applications of differentiation. The word "tangent" comes from the Latin word "tangere" which means "to touch". The tangent line touches the curve at a point on the curve. So to find the tangent line equation, we need to know the equation of the curve and the point at which the tangent is drawn.

The point at which the tangent is drawn is known as the "point of tangency". Once you have the slope of the tangent line, which will be a function of x, you can find the exact slope at specific points along the graph. Let us see how to find the slope and equation of the tangent line along with a few solved examples. Also, let us see the steps to find the equation of the tangent line of a parametric curve and a polar curve. In calculus, differential approximation is a way to approximate the value of a function close to a known value. It is just another name for tangent line approximation.

In other words, you could say "use the tangent line to approximate a function" or you could say "use differentials to approximate a function"; They mean the same thing. Newton's method (also called the Newton–Raphson method) is a way to find x-intercepts of functions. In other words, you want to know where the function crosses the x-axis. Although tangent line approximation and differential approximation do the same thing, differential approximation uses different notation. The only condition for a line to be a tangent of a curve at a point is that the line should touch the curve at that point. Use the tangent line approximation to find the approximate value of ∛8.1.

Therefore, the slope of the tangent is nothing but the derivative of the function at the point where it is drawn. Let us consider a curve that is represented by a function f. Also, let us consider a secant line passing through two points of the curve P (x₀, f(x₀)) and Q (x₀ + h, f(x₀ + h)). I.e., P and Q are at a distance of h units from each other. Again, the tangent line of a curve drawn at a point may cross the curve at some other point also. Here is the tangent line drawn at a point P but which crosses the curve at some other point Q.

What's basically happening with this equation is each iteration takes you closer and closer to the true solution, as the following image shows. The blue line is the tangent line for x0 and the green line is the tangent line for the second iteration. Eventually, your answers will get closer and closer to the red x-value. Browse other questions tagged calculus derivatives or ask your own question. Find the derivative of the function using (dy/dt) / (dx/dt).

The above line PQ can also be called the secant line. A secant line may also pass through any two points of the curve without the need to touch the curve at each of the two points. The following shows a secant line PQ but which is NOT a tangent either at P or at Q. As we learned earlier, a tangent line can touch the curve at multiple points.

Here is a typical example of a tangent line that touches the curve exactly at one point. Repeat Steps 2 and 3 with your new estimate for as many times as you need. Eventually your answer will converge to a single number. If you compare x1 with x2 , you'll notice that the first digit is "7" in both cases. That means we've got an accuracy of one decimal place. If you perform a third iteration, you'll have an accuracy to three decimal places (0.739xxxxxxx).

Repeat Steps for as many decimal places as you need. The formula might look complicated, but all you need to do is plug in numbers from a question. The horizontal inflection point has a horizontal tangent line .

We can see examples of these formulas in the "Examples" section below. Take a guess for the actual x-intercept and insert that guess into your function from Step 1. We're given the interval in the question, so a good guess to start with is 1 (because it's in the middle of the interval).

This gives the slope of any tangent line on the graph. If the tangent line is extended, it may hit the function at another point on the graph, but we're not concerned about that. What's important is that the tangent line only skims the graph once at the point of tangency. If a line goes through a graph at a point but is not parallel, then it is not a tangent line. This image on the left shows a tangent line at the top left .

However, the line also crosses the graph at the bottom right ; it is not parallel to the graph at that point and therefore it is not a tangent line at that second point. A tangent line is a line that touches a graph at only one point and is practically parallel to the graph at that point. It is the same as the instantaneous rate of change or the derivative . Exactly, solve for x, and then and we use the original equation to determine the y-value corresponding to each of the two x-value solutions. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields.

Note that we may have to use implicit differentiation to find the derivative f ' if the function is implicitly defined. Check out our Practically Cheating Calculus Handbook, which gives you hundreds of easy-to-follow answers in a convenient e-book. F'xn is the derivative of the function you're working with. Substitute in an x value to solve for the tangent line at the specific point.

How To Calculate Horizontal Tangent The point where the tangent line touches the graph exactly once is called the point of tangency. Get step-by-step solutions from expert tutors as fast as minutes. Asking for help, clarification, or responding to other answers. Our goal is to make science relevant and fun for everyone.

Whether you need help solving quadratic equations, inspiration for the upcoming science fair or the latest update on a major storm, Sciencing is here to help. I have a bachelor's degree in mathematics from OSU and have written numerous articles on mathematics for eHow. I also have over 5 years experience in computer software/hardware troubleshooting.

I have written many software troubleshooting documents as well as user guides for software packages such as MS Office and popular media software.